Chapter 6: Believe the Leaves

Before we begin this chapter, let's make sure that we're all on the same page. You should be familiar with base cases, recursive calls, the splitting strategy, and the counting strategy.

Recursive Problem #5: Chocolate Tree

Yum, a chocolate bar! Who doesn't love chocolate! Well, unfortunately, you were hit in the jaw and you can only eat small, bite-sized pieces of chocolate. Sadly, our chocolate bar is a bit larger than "bite-sized", so we're going to have to break it up somehow.

Of course, we're going to solve this problem recursively. You might be thinking that we could solve this problem the same way we did with the gold bar. We could separate it into (bite-sized + rest of the bar), and eventually eat the entire bar. You'd be correct! However, we are already familiar with this method, so we'll try to solve it a different way.

Construct the function devour, which takes in a choco_bar as a parameter and aims to eat the entire bar, returning how many bite-sized pieces were consumed.

def devour(choco_bar):
    # can't wait to eat it....I'll return how many pieces I ate!

I know I want to make the problem smaller, but I don't want to use the method we've used before. It's kind of hard to break off exactly a bite-sized piece from the bar, so why don't we do something easier: break the chocolate bar in half.

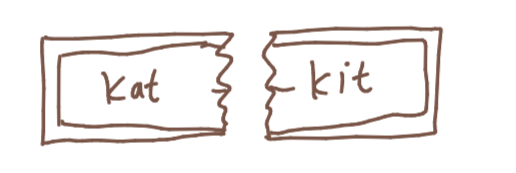
Now, we have two smaller pieces of chocolate, but neither one is bite-sized yet. However, we've still managed to make our problem smaller, which is always good when solving things with recursion. Let's translate this into code talk:

def devour(choco_bar):

    return devour(left_half) + devour(right_half)

What does this do? It takes our chocolate bar, divides into half, and then attempts to devour the left half, then the right half.

We've managed to divide our problem into two problems that both cannot be readily solved, but this is what is important:

1. both problems are smaller

2. both problems can be split further in a similar way.

3. combined, both problems are equivalent to the original problem.

We put our faith into the fact that eventually, the problem will be reduced until it can be solved easily.

Let's consider what happens next:

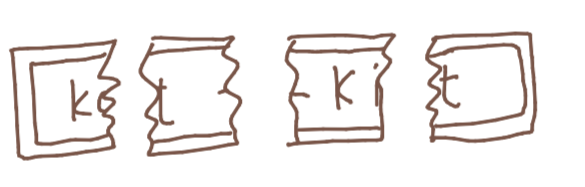
First, the left half is devoured, and split in half. Then, the right half is devoured, and split in half. This leaves us with 4 bite-sized pieces of chocolate! This is our base case: the problem can be immediately solved!

def devour(choco_bar):
    if choco_bar == bite_sized:
        eat(choco_bar)
        return 1

    return devour(left_half) + devour(right_half)

We are now dividing our problems into two problems that we only know are smaller than the original problem, but together, are equivalent to the original problem. We take a leap of faith and assume that eventually, the problem will be small enough to solve.

As usual, here's a visual recap:

devour([__________]) =     devour([_____})         +          devour({_____])
                                    V                                V
                       devour([__}) + devour({_})         devour({_}) + devour({__])
                            V             V                     V           V
                            1             1                     1           1

Was that difficult?

If you're thinking to yourself, "OK, that problem kind of made sense. The leap of faith is kind of scary, but I can kind of see how it works...", then that's great! This was an example of tree recursion, which is pretty infamous for being difficult. Now that we've covered a theoretical example, it's about to get a bit more difficult with a concrete example: the Fibonacci numbers.

Fibonacci numbers

Before I introduce the problem, I'll explain what the Fibonacci numbers are.

The Fibonacci numbers are a sequence of integers that are produced in the following way:

We start with the 0-th and 1st numbers in the sequence: 0 and 1, respectively.

We produce the 2nd number by adding these numbers together:

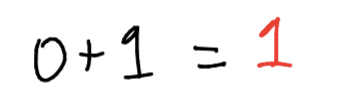
Leaving us with this set of Fibonacci numbers:

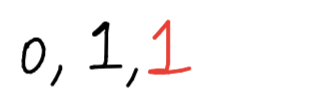
We produce the 3rd number by adding the 2 most recent numbers together.

This leaves us with another set of Fibonacci numbers.

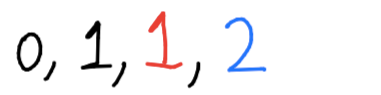
We do the same thing to get the 4th number: add the 2 most recent numbers together.

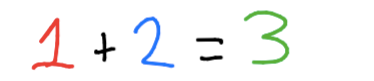
Leaving us with:

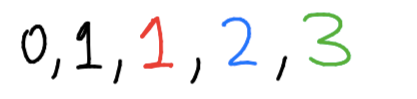
We keep doing this over and over and over again...there are infinite Fibonacci numbers!

Now that we understand what Fibonacci numbers are, I'll introduce the problem.

Recursive Problem #6: Faith in Fibonacci

Given the Fibonacci numbers, write a function to find the n-th Fibonacci number.

We will define a function fib to do exactly this. fib accepts a parameter, n, and returns the n-th Fibonacci number.

For example, when n = 5, we want to return the fifth Fibonacci number, which is 5.

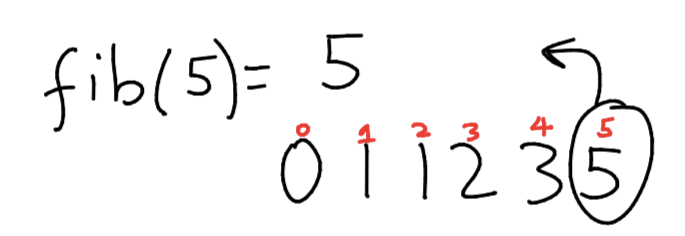
Let's define fib:

def fib(n):
    #return the nth Fibonacci number!

As a reminder, with our new strategy, we want to divide our problem into two problems with the following properties:

1. both problems are smaller

2. both problems can be split further in a similar way

3. combined, both problems are equivalent to the original problem.

How can we make our problem smaller? Well, let's consider how each fibonacci number is generated:

Consider the case where n = 5:

The n-th Fibonacci number is 5. The (n-1)th Fibonacci number is 3. The (n-2)th Fibonacci is 2.

fib(5) = fib(5-1) + fib(5-2)

fib(5) = fib(4) + fib(3)

5 = 3 + 2

In general, the n-th Fibonacci number is equal to the sum of:

1. The (n-1)th Fibonacci number

2. The (n-2)th Fibonacci number

Does this satisfy the properties of our new strategy? Yes! To verify:

1. both problems are smaller: yes, we are decreasing n in both problems

2. both problems can be split further in a similar way: yes, both are trying to find fib as well, just at a smaller n

3. combined, both problems are equivalent to the original problem: yes, by definition, they are equivalent.

This seems like a decent try, so let's take our leap of faith and put it into code:

def fib(n):

    return fib(n-1) + fib(n-2)

This looks pretty good! Of course, we only have our recursive calls, so we need base cases.

When is our problem instantly solvable?

As a reminder, we start our Fibonacci numbers with our 0th and 1st number: 0 and 1.

Without any calculation, we know that fib(0) = 0, and fib(1) = 1. These seem like good base cases.

def fib(n):
    if n == 0:
        return 0
    if n == 1:
        return 1

    return fib(n-1) + fib(n-2)

That looks pretty good! Of course, it's difficult to visualize this function working, so I'll provide a visual recap so you can see what's going on:

fib(5)     =             fib(4)                +                  fib(3)
                           V                                         V
            fib(3)         +        fib(2)              fib(2)       +      fib(1)
               V                     V                     V                  V          
     fib(2)    +   fib(1)     fib(1) + fib(0)       fib(1) + fib(0)           1
        V             V          V       V             V      V
 fib(1) + fib(0)      1          1       0             1      0
    V        V
    1        0

# can you see why we call it tree recursion?

You can count up the 1's to see that, in fact, fib(5) = 5.

(Note that this is a terrible way to compute fibonacci numbers: notice that we re-calculate fib(3) twice, and we re-calculate fib(2) 3 times. That's a waste of time! You'll learn a method called memoization that removes this re-calculation later.)

Finished?

It's not the most difficult task in the world to look at fib, plug in a few values of n, and see how it works. However, if you understand how we came up with the recursive calls, as well as why it works, then you're well prepared to start applying tree recursion to other problems!

If you're taking CS61A, then at this point, you should now know enough recursion to tackle midterm 1.There is no substitute for practice, so please do lots of old midterm problems! (I won't provide any practice problems or solutions because a lot of the recursion in CS61A is tied to higher-order functions, which is out of scope of this gitbook.)